Tổng Hai Vecto Bằng 0
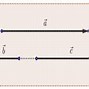
Trong mặt phẳng tọa độ Oxy; cho hai vectơ a→-1;1;b→2;0. Tính cosin của góc giữa hai vectơ a→ và b→
Công thức tính Tích vô hướng của hai vecto trong không gian (cực hay)
Bài viết Công thức tính Tích vô hướng của hai vecto trong không gian với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Công thức tính Tích vô hướng của hai vecto trong không gian.
ĐỀ THI, GIÁO ÁN, SÁCH LUYỆN THI DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 10
Bộ giáo án, bài giảng powerpoint, đề thi, sách dành cho giáo viên và gia sư dành cho phụ huynh tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official
Tổng đài hỗ trợ đăng ký : 084 283 45 85
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi online, Bài giảng....miễn phí. Tải ngay ứng dụng trên Android và iOS.
Theo dõi chúng tôi miễn phí trên mạng xã hội facebook và youtube:
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
tich-vo-huong-cua-hai-vecto-va-ung-dung.jsp
Giải bài tập lớp 10 sách mới các môn học
Công thức, cách tính góc giữa hai vecto (cực hay, chi tiết)
Bài viết Công thức, cách tính góc giữa hai vecto với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Công thức, cách tính góc giữa hai vecto.
ĐỀ THI, GIÁO ÁN, GÓI THI ONLINE DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 12
Bộ giáo án, đề thi, bài giảng powerpoint, khóa học dành cho các thầy cô và học sinh lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official
phuong-phap-toa-do-trong-khong-gian.jsp
Giải bài tập lớp 12 sách mới các môn học
Công thức tính Tích vô hướng của hai vecto trong không gian (cực hay)
Bài giảng: Các dạng bài tập hệ trục tọa độ trong không gian - Cô Nguyễn Phương Anh (Giáo viên VietJack)
Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),
b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.
b) So sánh a→.(b→.c→) và (a→.b→ ) c→
c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )
c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)
⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11
b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)
a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)
Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→
+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)
d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)
u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0
(u→ ,a→ )=600⇔cos(u→ ,a→ )=1/2
Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=1200,
|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |
Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos(a→ ,b→ )
Ta có: |a→ + b→ |2=(a→ + b→ )2=a→ 2+2a→ .b→ +b→ 2
=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7
|a→ -2b→ |2 =|a→ |2+4|b→ |2-4|a→ |.|b→ |.cos(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52
Bài 3: Trong không gian Oxyz, cho các điểm A(2; -1; 1), B(3; 5; 2), C(8; 4; 3), D(-2; 2m+1; -3)
a) Chứng minh tam giác ABC là tam giác vuông
b) Tìm m sao cho tam giác ABD vuông tại A
c) Tính số đo góc A của tam giác ABC
a) Ta có: AB→=(1;6;1); BC→=(5;-1;1)
b) AB→=(1;6;1); AD→=(-4;2m+2; -4)
Tam giác ABD vuông tại A ⇔AB→.AD→=0
Bài 1: Cho các vectơ u→(u1;u2;u3) và v→(v1;v2;v3), u→. v→=0 khi và chỉ khi:
Bài 2: Cho hai vectơ a→ và b→ tạo với nhau góc 600 và |a→| =2; |b→| =4. Khi đó |a→ + b→ | bằng:
|a→ + b→ |2=(a→ + b→ )2=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos(a→ + b→ )
Bài 3: Cho a→(-2;1;3), b→(1;2;m). Với giá trị nào của m để a→ vuông góc với b→ ?
a→ vuông góc với b→ khi và chỉ khi a→ . b→=0
Bài 4: Tính cosin của góc giữa hai vectơ a→ và b→ biết a→(8;4;1), b→(2;-2;1)
Bài 5: Cho tam giác ABC với A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Khi đó số đo của góc BACˆ bằng:
Bài 6: Cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Khi đó số đo của góc giữa hai đường thẳng AB và CD là :
Gọi góc giữa 2 đường thẳng AB và CD là α
Bài 7: Trong không gian với hệ toạ độ Oxyz, cho hai vecto a→; b→. Trong các khẳng định sau, khẳng định nào đúng:
A. a→ .|b→ |=|a→ |.b→ với mọi a→ ; b→
B. ( a→ b→ )2=a→ 2 . b→ 2 với mọi a→ ; b→
C. |a→ . b→ | ≤|a→ |.|b→ | với mọi a→ ; b→
D. a→ . b→ =0 khi và chỉ khi a→ = 0→ hoặc b→ = 0→
d) a→ b→ =0 nhưng a→ ≠ 0→ hoặc b→ ≠ 0→
Bài 8: Trong không gian Oxyz, cho a→(-1;2;-3), b→(3;3;4), c→(5;0-1). Giá trị của a→ (b→ + c→ ) là:
⇒ a→ (b→ + c→ )=-1.8+2.3-3.3=-11
Bài 9: Cho 3 điểm A(2; 1; -3), B(–2; 2; –6), C(5; 0; –1). Tích AB→. AC→ bằng:
⇒ AB→ . AC→ =-4.3+1.(-1)-3.2=-19
Bài 10: Trong không gian với hệ tọa độ Oxyz, điều kiện để a→ vuông góc với b→ là gì ?
A. a→ . b→ =0 B. [ a→ , b→] = 0→
C. a→ + b→ = 0→ D. a→ - b→ = 0→
Bài 11: Cho hai vecto a→; b→thay đổi nhưng luôn thỏa mãn |a→|=5; |b→ |=3. Giá trị lớn nhất của |a→ -2 b→ | là:
Ta có: |a→ - 2 b→ |2 = ( a→ - 2 b→ )2 = | a→ |2 + 4| b→ |2 - 4| a→ |.| b→ |.cos( a→ ; b→ )
| a→ -2 b→ | lớn nhất ⇔ | a→ - 2 b→ |2 lớn nhất ⇔cos( a→ ; b→ )=0
Khi đó: | a→ - 2 b→ |2=| a→ |2+4| b→ |2=25+4.9=61
Bài 12: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ a→(-1;1;0), b→(1;1;0), c→(1;1;1,). Trong các mệnh đề sau, mệnh đề nào sai ?
⇒ Hai vecto c→ ; b→ không vuông góc với nhau
Bài 13: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có AB→=(-3;0;4), AC→=(5;-2;4). Độ dài trung tuyến AM là:
Ta có: AB=|AB→ |=5; AC=|AC→ |=√45
Ta có: BC2=AB2+AC2 - 2AB.AC.cosBACˆ =68
Bài 14: Cho | a→ |=2; | b→ |=5, góc giữa hai vectơ a→ và b→ bằng (2π)/3, u→ = k a→ - b→; v→ = a→ + 2 b→. Để u→ vuông góc với v→ thì k bằng?
⇒ u→ . v→ =(k a→ - b→ )(a→ +2 b→ )=k a→ 2-2 b→ 2+(2k-1) a→ . b→
Ta có: a→ . b→ =| a→ |.| b→ |.cos( a→ ; b→ )=2.5.cos(2π/3)=-5
⇒ u→ . v→ =4k-2.25+(2k-1).(-5)=-6k-45
Giả thiết: u→ và v→ vuông góc với nhau ⇒ u→ . v→ =0
Bài 15: Trong không gian với hệ tọa độ Oxyz, cho a→=(x;2;1), b→ =(2;1;2), Tìm x biết cos( a→ , b→ )=2/3.
Bài 16: Trong không gian với hệ tọa độ Oxyz, cho A→ (-2;2;-1), B→ (-2;3;0), C→ (x;3;-1). Giá trị của x để tam giác ABC đều là:
AB→ =(0;1;1); AC→ =(x+2;1;0); BC→ =(x+2;0;-1)
Tam giác ABC đều ⇔ BACˆ= ABCˆ=600
Bài 17: Cho hai vecto a→; b→ tạo với nhau một góc 600. Biết độ dài của hai vecto đó lần lượt là 5 và 10. Độ dài của vecto hiệu a→ - b→ là:
Ta có: | a→ - b→ |2=( a→ - b→ )2=| a→ |2+| b→ |2-2| a→ |.| b→ |.cos( a→ ; b→ )
Bài 18: Trong không gian với hệ tọa độ Oxyz,cho tam giác ABC với A(-4;3;5), B(-3;2;5) và C(5;-3;8). Tính cos(AB→ ; BC→ ).
AB→ =(1; -1;0); BC→ =(8; -5;3)
Bài 19: Trong không gian với hệ toạ độ Oxyz, tam giác ABC có A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Số đo của góc B là:
Bài 20: Trong không gian Oxyz, cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn điều kiện x2+y2+z2=4; m2+n2+p2=9. Vecto AB→ có độ dài nhỏ nhất là:
Dấu bằng xảy ra khi O nằm ngoài đoạn AB.
Công thức, cách tính góc giữa hai vecto (cực hay, chi tiết)
Phương pháp 1: Sử dụng định nghĩa góc giữa hai vectơ
Định nghĩa góc giữa hai vectơ: Cho hai vectơ đều khác vectơ-không. Từ một điểm O bất kỳ, ta vẽ các vectơ . Khi đó số đo của góc AOB, được gọi là số đo góc giữa hai vectơ , hoặc đơn giản là góc giữa hai vectơ .
Phương pháp 2: (Áp dụng trong hệ tọa độ) Tính cos góc giữa hai vectơ, từ đó suy ra góc giữa 2 vectơ.
Chú ý: Góc giữa hai vectơ thuộc [0°;180°]
Ví dụ 1: Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ:
- Nhớ lại khái niệm hai vectơ bằng nhau ở chương 1: Hai vectơ bằng nhau khi chúng cùng hướng và cùng độ dài.
- Trên tia đối của tia CB lấy D sao cho CB = CD.
Ví dụ 2: Cho các vectơ Tính góc giữa hai vectơ .
Vậy góc giữa hai vectơ là góc α ∈ [0°;180°] thỏa mãn .
Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho hai vectơ . Tính góc giữa hai vectơ .
Ví dụ 4: Cho hai vectơ có độ dài bằng 1 và thỏa mãn điều kiện . Tính góc giữa hai vectơ .
Vì (bình phương vô hướng bằng bình phương độ dài)
Ví dụ 5: Cho các vectơ thỏa mãn . Góc giữa vectơ và vectơ là
Bài 1. Tính góc giữa vecto a và vectơ c, biết vectơ c→=a→−b→ và cho các vectơ a và b thoả mãn |a| = 4, |b| = 2.
Nên c2 = (a – b)2 = a2 – 2ab + b2 = |a|2 – 2|a| . |b| . cos(a,b) + |b|2
Suy ra c2 = 42 – 2.4.1.cos60o + 22 = 3 hay |c| = 3.
Ta lại có: a . c = a . (a – b) = a2 – a . b hay a . c =3
Do đó a . c = |a| . |c| . cos (a, c)
Vậy góc giữa 2 vectơ bằng 30o.
Bài 2. Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là 1. Gọi M là trung điểm của canh AB. Tính góc giữa hai vectơ OM→, BC→.
Lấy N là trung điểm của AC suy ra MN // BC.
Ta có: OM→ , BC→=OM→ , MN→=180°−OMN^
Xét tam giác OMN có OM = ON = 12; MN = 12BC = 22
Suy ra cosOMN^=12 hoặc OMN^=60°.
Bài 3. Tính góc giữa 2 vectơ a và b, biết rằng 2 vectơ a và b có độ bài bằng 1 và thoả mãn điều kiện |3a + 2b| = 7.
Ta có: 3a+2b=7 hay 3a⋅2b2 =7 nên 9a2 + 12b + 4b = 7
Vì a2 = |a|2 =1; b2 = |b|2 =1.
Nê 4 . 1 + 12ab + 9 . 1 = 7 nên 12ab = 7 – 4 – 9 = –6 hay ab = −12.
Vậy góc giữa 2 vectơ a và b là 120 độ.
Bài 4. Cho hình thoi ABCD có BAD^=120°. Tính góc giữa hai vectơ DC→ và AD→.
Ta có AB // DC và AB = DC (vì ABCD là hình thoi)
Suy ra DC→=AD→ nên DC→, AD→=AB→, AD→.
Bài 5. Cho tứ diện ABCD có AC = BD = 2a. Gọi M, N lần lượt là trung điểm BC, AD. Biết rằng MN = a3. Tính góc giữa AC và BD.
Gọi I là trung điểm của AB, ta có IM = IN = a
Áp dụng định lý của Cosin cho tam giác IMN ta có:
cosMIN^=IM2+IN2−MN22 . IM . IN = a2+a2−3a22 . a . a=−12
Vậy góc giữa AC và BD bằng 60 độ.
Bài 6. Cho các vectơ a→=i→+j→ ; b→=2i→+3j→. Tính góc giữa hai vectơ a→,b→.
Bài 7. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a→=2;5; b→=3; 7. Tính góc giữa hai vectơ a→; b→.
Bài 8. cho hai vectơ a→;b→ có độ dài bằng 1 và thỏa mãn điều kiện 3a→+5b→=9. Tính góc giữa hai vectơ a→;b→.
Bài 9. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a3, SA vuông góc với mặt phẳng đáy tại A, SA = a2. Tính góc giữa đường thẳng SC và mặt phẳng ABCD.
Bài 10. Cho hình chóp S.ABCD có đấy ABCD là hình bình hành với BC = 2a, SA vuông góc với mặt phẳng đáy, Góc giữa hai đường thẳng SD và BC nằm trong khoảng nào?
Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác khác:
Lời giải bài tập lớp 10 sách mới:



